|
|
|
|
Euler's Totient Function
Euler's totient function is of major interest in number theory. For example, its use enabled mathematicians to build a code which is almost impossible to break, even though the key is made public. The totient function, also known as the Phi function or φ(n), is the number of positive integers not exceeding n that have no common divisors with n (other than the common divisor 1). For example, φ(12) = 4, since the four numbers 1, 5, 7, and 11 do not share a common divisor with 12.
This mathematical function also has implications for numbers discussed elsewhere on this website:
|
Euler's phi (or totient) function of a positive integer n is the number of integers in {1,2,3,...,n} which are relatively prime to n.
The 703 triangle and the 541 Israel star are both 37 rows deep, with a perimeter of 108. The area of the 37:108 triangle is 1998.
|
Genesis 1:1 -- φ(1998) = φ(703)
Given that we are presently in the astrological age of Pisces, recall the story of Jesus and the 153 fish from John 21:1-11
Number 144 and it's anagrams also display interesting properties:
- φ(888) = 288
- φ(288) = φ(153)
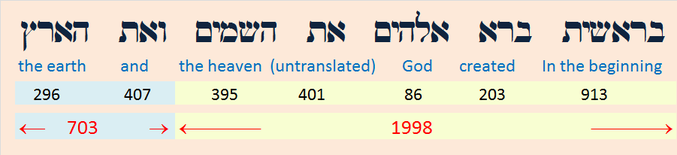
- 153 + 135 + 315 + 351 + 513 + 531 = 1998 (In the beginning God created the heaven)
- 432 + 423 + 324 + 342 + 243 + 234 = 1998
- 153 + 432 = 585
- φ(585) = 288
Number 144 and it's anagrams also display interesting properties:
- 144 + 414 + 441 = 999
- 1998 = 2 x 999
- φ(999) = φ(1998)
When you see “.999 fine silver” or “999” stamped on an item, it is considered pure silver. Sterling is 92.5% silver and 7.5% alloy.
|
"The words of the LORD are pure words: as silver tried in a furnace of earth, purified seven times." Psalm 12:6
|
Contact |
|